Interaktive NPR-Darstellung von Metalloberflächen in Airbrushtechnik
Dieses Dokument ist auch in einer
PDF-Version verfügbar.
Inhalt
Einleitung
Bei der Darstellung dreidimensionaler Objekte und Szenen gibt es in der Computergraphik zwei wichtige Schwerpunkte: Die Erstellung photorealistischer Bilder einerseits, sowie mehr oder weniger skizzierte Grafiken mit Schwerpunkt auf einer möglichst guten Erkennbarkeit der Details andererseits. Daneben gibt es viele Ansätze, auch künstlerische Techniken nachzubilden, welche unter dem Sammelbegriff des nicht-photorealistischen Renderings (NPR) gerade in letzter Zeit einen deutlichen Aufschwung erfahren haben.
Zu den verbreitetesten NPR-Techniken gehört das Cool-to-Warm-Shading, bei dem die normale Beleuchtung mit Schattierungen durch eine Beleuchtung mit warmen Licht und entgegengesetztem kaltem Gegenlicht ersetzt wird; diverse texturbasierte Verfahren zur Nachbildung von refraktierenden, spiegelnden und metallischen Oberflächen sowie das Cartoon-Rendering. Zu Letzterem gibt es eine Vielzahl an Verfahren, deren gemeinsame Hauptmerkmale das Nachzeichnen von Objektkanten und Silhouetten zusammen mit der Verwendung von wenigen Helligkeits- und Farbstufen für Schattierungen bilden. Mittlerweile gibt es auch Ansätze, Metasymbole für Bewegungen und Emotionen wie Staubwolken, Bewegungslinien oder Gedankenblitze geeignet in das Cartoon-Rendering einzubinden.
Eine andere Klasse nichtrealistischer Darstellung bilden Verfahren, die weniger auf eine klare Darstellung sondern mehr auf die Nachbildung künstlerischer Stilrichtungen abzielen. Dazu zählen Kupferstiche und Radierungen, bei denen die Darstellung von Helligkeit und Konturen vorwiegend durch die Dichte und Lage der verwendeten Punkte bzw. Linien erzielt wird, ebenso wie Schraffurzeichnungen, bei denen mit unterschiedlich breiten Linien Schattierungen realisiert werden. In der Regel folgen diese Linien den Oberflächen, was in den verwendeten Verfahren in der Regel eine aufwendige Vorverarbeitung erfordert. Vergleichsweise einfach sind dagegen Techniken, welche Kohlezeichnungen nachbilden und auf Texturen zur Modulation der Schattierungen entsprechend Papier und gezeichneter Oberflächen beruhen.
Den Abschluß bilden Painterly-Verfahren zur Nachbildung von Malereien. Die Farbe und mitunter auch Form und Lage der Pinselstriche werden dabei einem Referenzbild entnommen. Für animierte Bilder ist allerdings auch hier ein gewisser Aufwand an Vorverarbeitung nötig, sofern man die Pinselstriche den Objekten folgen lassen möchte.
Bisher weitgehend unbeachtet blieb dagegen der Airbrush, mit dem es im Bereich der darstellenden Künste ein Medium gibt, welches Abstraktion erfolgreich mit Realismus verbindet. Eine genauere Analyse zeigt jedoch, daß viele Verfahren mit dem Airbrush über Entsprechungen in der Computergraphik verfügen oder leicht in diese zu übernehmen sind. Darüber hinaus eignen sie sich besonders für eine Realisierung mittels gängiger Rasterisierungshardware, was sie speziell für geschwindigkeitskritische, interaktive Anwendungen geeignet macht. Die im folgenden beschriebene vergleichsweise einfache Erzeugung semirealistischer Graphiken im Airbrushstil bietet hier eine interessante Alternative zu photorealistischen Verfahren, da letztere für qualitativ hochwertige Bilder schnell einen immensen Aufwand erfordern.
Der Schwerpunkt wird im Folgenden auf der Darstellung von Metalloberflächen samt ihrer vielfältigen Erscheinungsformen liegen. Aus der Fülle gestalterischer Techniken und physikalischen Grundlagen werden diejenigen vorgestellt, die für die Umsetzung relevant sind.
Airbrush als gestalterisches und künstlerisches Medium
Einsatzgebiete
Von der Lackierung in der gewerblichen Produktion über die Retusche von Photos und Erstellung realistisch wirkender Bilder bis hin zu freier künstlerischer Gestaltung findet der Luftpinsel Gebrauch. Besonders beliebt ist er bei der Erstellung von Illustrationen und Werbegraphiken aufgrund der perfekt wirkenden Farbverläufe und der klaren Darstellung unter Verzicht auf störende Details. Auch zur Ergänzung bestehender Liniengraphiken aus Konstruktionsplänen oder der Colorierung von Cartoons wird er deshalb öfters eingesetzt.
Farbauftrag
Um Verwirrungen zu vermeiden, soll im Folgenden - ähnlich wie in [1] - zwischen der Farbe als Eigenschaft und "Farbe" als Material unterschieden werden. Letztere wird für den Rest des Dokuments ungeachtet des tatsächlichen Aufbaus als Pigment bezeichnet, wohingegen mit Farbe die Farbe von Pigmenten, Oberflächen oder Licht gemeint ist.
Im Airbrush werden vorwiegend zwei Pigmenttypen eingesetzt: Lasuren und Tuschen mit subtraktiver Farbmischung und geringer Deckkraft sowie deckende Pigmente, deren Mischverhaltem direkt dem Anteil des aufgetragenen Pigments an der Oberfläche entspricht. Seltener werden auch Glimmerpigmente mit additivem Mischverhalten verwendet, aufgrund des stark metallischen Glitzereffekts sind sie vorwiegend bei Effektlackierungen anzutreffen.
Lasuren werden aufgrund ihrer mangelnden Deckfähigkeit stets von hellen nach dunklen Farbtönen angewendet, wohingegen deckende Pigmente auch ein Vorgehen in umgekehrter oder beliebiger Reihenfolge erlauben. Auffällig ist, daß in beiden Fällen die meist weiße Farbe des Untergrunds mit in die farbliche Gestaltung eingeht. Dies liegt weniger an dem geringeren Arbeitsaufwand oder der begrenzten Deckfähigkeit des eingesetzten Pigments, sondern vor allem an der meist unübertroffen hohen Strahlkraft reinen Papiers als auch vieler grundierten Oberflächen im Vergleich zu den eingesetzten Pigmenten.
Aufgrund des hohen Aufwands für das Reinigen des Airbrushs beim Wechsel des Pigments als auch aus gestalterischen Gründen beschränken sich Airbrushbilder meist auf wenige Grundfarben. Aus diesen entsteht dann durch Mischung mittels unterschiedlich starkem Auftrag des Pigments die vollständige Farbpalette. Stärke, Verlauf und Breite des Pigmentauftrags können dabei durch Variation des Verhältnisses von Pigment und Luft, dem Sprühwinkel und dem Abstand zur Oberfläche fein dosiert werden.
Während vollständig gleichförmige Farbflächen sehr leicht erstellbar sind erfordert ein großflächiger Farbverlauf viel Geschick und Übung. Aus diesem Grund sind weite, gleichmäßige Farbverläufe eher selten anzutreffen. Wesentlich bedeutendere Folgen hat jedoch die Einschränkung, daß ein Airbrush das Pigment selbst mit dem präzisesten Gerät stets auf einer Fläche verteilt.
Aus diesem Grund werden meist zusätzliche Mittel eingesetzt: Mit einem Pinsel lassen sich Details einfügen, feine Linien können mit Aquarell-, Filz- und Tuschestiften ergänzt werden. Ebenso kann einem gleichförmigem Pigmentauftrag durch Wischen, Tupfen und Radieren mit den unterschiedlichsten Materialien mehr Struktur verliehen werden [2,3,5].
Bildgestaltung
Am Anfang steht meist eine Vorzeichnung anhand eines freien Enturfs oder einer Photographie. Zur Erhöhung des realistischen Eindrucks und der beabsichtigten Wirkung wird eine Perspektive mit ein, zwei oder drei Fluchtpunkten eingesetzt. Darüber hinaus wird durch die Wahl einer warmen oder kalten, gebrochenen oder satten Farbpalette die Stimmung des Bildes festgelegt.
Während ein Airbrush von Haus aus für weiche, organische Verläufe geeignet ist sind für die Darstellung mehr oder minder harter Kanten Hilfsmittel nötig. Aus diesem Grund gehören Masken verschiedenster Art zur Eindämmung des Sprühstrahls zum zweitwichtigsten Werkzeug eines Künstlers. Zum Maskieren eignen sich spezieller Decklack, aber auch Folie, geschnittenes oder gerissenes Papier, Watte sowie fast jeder sonstige Gegenstand. Je nach Abstand zum Untergrund und der Randschärfe dieser Maske ergeben sich unterschiedliche Verläufe und Strukturen. Darüber hinaus lassen sich Schablonen durch Verschieben auch für Abstufungen und Schlagschatten einsetzen.
Reflektierte Lichter werden anhand eines Referenzbildes oder mittels gedachter Lichtquellen umgesetzt. Meist verfügen diese über parallel auftretende Lichtstrahlen, wie sie vor allem für Sonnenlicht als bedeutendste Lichtquelle zutreffen. Für gestalterische Zwecke sind Abweichungen von der Realität allerdings durchaus gängig.
Besondere Sorgfalt erfordert die Umsetzung von Metall. Am besten verdeutlichen dies die Zitate einiger bekannter Künstler: "Wichtig ist, [...] daß Licht und Schatten auf Metall wie in einem Spiegel projiziert werden, wobei sie der äußeren Form des Gegenstands folgen."
[2] sowie "Es gibt keine konkrete Darstellung von Gold, sondern nur die Farben, die sich in der goldenen Fläche spiegeln.[...]"
[3]. Streng physikalisch trifft dies zwar auch auf alle anderen Materialien zu, ist dort aber für die menschliche Wahrnehmung weitgehend unbedeutend.
Spiegelungen werden im Airbrush typischerweise nur stark idealisiert dargestellt. In Innenräumen ist dies meist das Abbild eines oder mehrerer Fenster, für im Freien stehende Objekte wird je eine Farbe für die Himmelshemisphäre sowie dem Boden gewählt, welche durch einen teils unregelmäßigen Farbverlauf am Horizont getrennt werden.
Die Wirkung sich selbst abschattender Oberflächen wird gerne überzeichnet, um den plastischen Eindruck zu betonen. Darüber hinaus finden Schatten nur spärlich Anwendung, etwa an eng benachbarten Stellen an denen sein Fehlen schnell auffallen würde, oder zur Hervorhebung von Objekten und ihrer Lage.
Spezielle Effekte
Spittering
Nicht immer ist ein homogener Farbverlauf ideal. Um rauhe Oberflächen wie Sand, Stein oder unedles, oxidationsanfälliges Metall darzustellen eignet sich ein gesprenkelter Pigmentauftrag besser. Dieser kann durch Verändern der Luftzufuhr erzielt werden. Falls nur wenige Flecken erzeugt werden sollen, etwa für einen Sternenhimmel oder beginnende Korrosion, kann das Pigment auch mittels Pinsel oder Bürste auf den Untergrund gespritzt werden.
Kratztechnik
Mittels Messer oder Sandpapier lassen sich Pigmentschichten abtragen, so daß die darunterliegende Farbe wieder zum Vorschein kommt. Neben der Herstellung feinster Details eignet sich diese Technik vor allem zur Darstellung gebürsteter und gefräster Oberflächen, bei denen zwar die Linienstruktur, nicht mehr aber einzelne Linien wahrnehmbar sind[6].
Spitzlichter
Ein generelles Problem fast aller Maltechniken ist der begrenzte Dynamikumfang der Pigmente, welcher für hoch reflektierende Oberflächen von Wasser und Metallen nicht ausreicht. Um sie dennoch darstellen zu können, werden die hellsten Bereiche zusätzlich mit Weiß (also dem hellsten verfügbaren Pigment) wolkenartig übersprüht, wodurch die Überstrahlung hellen Lichts in benachbarte Bereiche nachgebildet wird. Richtig eingesetzt entspricht dies durchaus dem Verhalten überbelichteter Bereiche in einer realen Kamera[2,3].
Sterneffekte
Optische Systeme zeigen oftmals, nicht selten sogar beabsichtigt, sternförmige Ausläufer mit 4, 6 oder 8 Ästen rund um helle Lichtquellen und Reflexionen. Dieser Effekt wird im Airbrush meist als Kombination von Sprühtechnik für den Kern sowie Kratztechnik für die Äste nachgebildet. Im Gegensatz zu den flächigen Reflexionen mit Glanzlichtern verdeutlicht er jedoch bevorzugt punktförmige Spitzlichter an besonders hochwertig polierten Oberflächen, kann aber auch mit flächigen Spitzlichtern kombiniert werden[3].

Beugungssterne und ein skizzierter Horizont sowie Einsatz von Masken, Radierer, Pinsel und Spittering (Quelle:
Airbrush-Galerie Kai Blume)
Eigenschaften von Metalloberflächen
Physikalisch
In Luft oder Vakuum (Brechungsindex=1) gelten für den als Betragsquadrat des Reflexionskoeffizienten R definierten Reflexionsgrad Rho mit Brechungsindex n folgende Fresnel-Formeln[7,9]:
Rparallel = (n2 * cos(a) - sqrt(n2 - sin(a)2)) / (n2 * cos(a) + sqrt(n2 - sin(a)2))
RSenkrecht = ((sqrt(n2 - sin(a)2) - cos(a))2) / (n2 - 1)
Dabei wird der Winkel a gegen die Oberflächennormale gemessen, Rparallel gilt für parallel und Rsenkrecht für senkrecht zur Reflexionsebene polarisiertes Licht. Diese vereinfachten Formeln gelten strenggenommen nur für nichtmagnetische Materialien, was aber für die folgenden qualitativen Betrachtungen keine Einschränkung darstellt.
Hier lassen sich zwei wichtige und zudem polarisationsunabhängige Eigenschaften ablesen: Erstens geht der Betrag des Reflexionskoeffizienten für flachen Lichteinfall gegen 1, wodurch das gesamte einfallende Licht unabhängig von der Farbe reflektiert wird. Zweitens beträgt der Reflexionskoeffizient für senkrechten Lichteinfall (n - 1) / (n + 1), so daß Farbe und Intensität des reflektierten Lichts nur vom frequenzabhängigen Brechungsindex abhängen.
In Metallen ist durch die frei beweglichen Elektronen zusätzlich der Leitungsstrom sowie in Folge die auftretende Dämpfung einfallender elektromagnetischer Wellen durch den elektrischen Widerstand des Metalles zu berücksichtigen. Dazu wird die reelle Dieelektrizitätskonstante epsilonr um einen imaginären Anteil erweitert, so daß auch der Brechungsindex n zu einer komplexen Zahl wird. Für den imaginären Anteil gilt bei Wellen mit Frequenz f:
Im(n) = sqrt(mur * sigma / (4 * pi * epsilon0 * f))
Hierbei sind als Materialparameter mur als relative Permeabilität, die Leitfähigkeit Sigma sowie die Vakuumdielektrizitätskonstante epsilon0 einzusetzen.
In weiten Teilen des sichtbaren Bereichs ist
n = sqrt(epsilonr * mur + i*sqrt(sigma * mur)/(4 * pi * f * epsilon0))
näherungsweise
Im(n) >> 1, woraus die hohe Reflektivität selbst bei senkrechtem Lichteinfall folgt.
Die Eindringtiefe T elektromagnetischer Wellen bis zu einem Abfall auf 1/e ihrer ursprünglichen Intensität ergibt sich zu
T = lambda / (4 * pi * Im(n) / Re(n))
wobei
lambda die Wellenlänge im Metall bezeichnet. Somit findet die Reflexion sichtbaren Lichts praktisch ausschließlich an der Oberfläche statt.[
7,
8]
Beispieleigenschaften einiger wichtiger Metalle für unpolarisiertes grünes Licht (lambda = 530 nm)
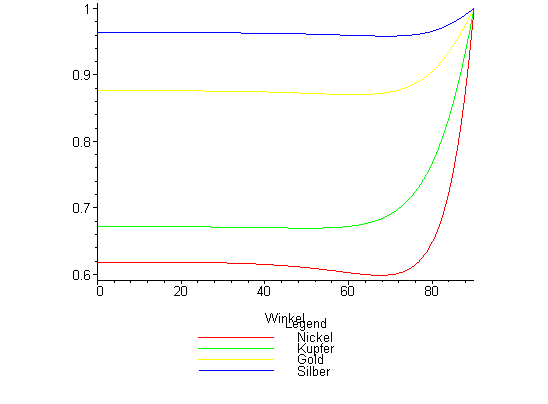
Winkelabhängigkeit des Reflexionsgrades
| Metall | Re(n) | Im(n) | Reflexionsgrad bei senkrechtem Einfall | Relative Eindringtiefe (lambda) |
|---|
| Nickel | 1,80 | 3,32 | 0,62 | 0,043 |
| Kupfer | 0,83 | 2,60 | 0,67 | 0,025 |
| Gold | 0,31 | 2,88 | 0,88 | 0,009 |
| Silber | 0,12 | 3,45 | 0,96 | 0,003 |
Strukturelle Eigenschaften
Da aufgrund der geringen Eindringtiefe praktisch keine Streuung des Lichts innerhalb des Metalls auftritt hängt das Reflexionsverhalten stark von der herstellungs- und verwendungsbedingten Oberflächenstruktur ab. Wichtige im Alltag vorkommende Feinstrukturen sind:
- Geätzte, leicht glitzernde Oberflächen mit mikroskopisch rauher isotroper Struktur
- Nahezu perfekt ebene polierte oder gewalzte Oberflächen, mitunter mit leichter Anisotropie
- Gegossene, eher matte Oberflächen mit rauher Struktur
- Gebürstete, gedrehte oder gefräste Bauteile mit stark anisotroper Reflexion und glatter Oberfläche
Anisotropie tritt bei den genannten Formen in einer stärkeren Reflexion in Abhängigkeit zur Bearbeitungsrichtung auf. Darüber hinaus wirken sich durch den hohen Reflexionsgrad auch leichte Variationen der Grobstruktur, wie sie durch Schrumpfungen an gegossenen Gegenständen, punzierten, gehämmerten und verbogenem Blechen sowie durch Applikationen wie Schrauben und Nieten entstehen, stark aus.
Entwurfskriterien
Neben der Berücksichtigung oben genannter Schlüsseleigenschaften sollte das zu entwickelnde Verfahren sich möglichst nahtlos in bestehende Anwendungen einfügen und kombinierbar mit anderen Verfahren sein. Dies bedeutet, daß es unabhängig von der gewählten Form der Verdeckungsberechnung anwendbar sowie möglichst keine Annahmen über die Tiefen-, Stencil-, Alpha- und Scissorstufen der Graphikhardware sowie dem gewählten Rendertarget vorraussetzen sollte. Bestehende 3D-Objekte sollten ohne manuelle Änderung direkt einsetzbar sein, ebenso die bisher verwendeten Lichtquellen und Transformationen.
Von speziellem Interesse war auch die Eignung für interaktive, animationsfähige Anwendungen. Somit sollten sich Änderungen der Objekt- und Beobachtungsposition sowie beliebiger Parameter kontinuierlich und mit gleichbleibender Bildqualität auswirken. Die verwendeten Parameter sollten intuitiv verständlich und leicht bedienbar sein, aus Geschwindigkeitsgründen sollte das Verfahren möglichst innerhalb eines Renderdurchgangs erfolgen und auf weiteres Postprocessing verzichten.
Simulation des Farbauftrags
Kern des Verfahrens ist die Nachbildung des Pigmentauftrags. Diese sollte orthogonal zu der Berechnung der Farbwerte und Intensitäten erfolgen, wodurch spätere Erweiterungen probemlos unterstützt werden.
Grundprinzip: Dithering im Bildraum
Für den fertigen Bildeindruck ist nur das Aussehen, nicht aber das Zustandekommen des Pigmentauftrags relevant. Das Aussehen hängt dabei direkt von dem Verhältnis der mit Pigment bedeckten zur unbedeckten Fläche ab, so daß der Farbauftrag mittels eines Ditheringverfahrens nachgebildet werden kann. Ein- und Ausgabedaten des Dithervorgangs sind jedoch keine Farbwerte, sondern die mittlere und lokal resultierende Intensität des Pigments. Das Verfahren läuft im Bildraum ab, um eine gleichbleibende und objektunabhängige Streuauflösung wie auf dem Papier zu gewährleisten. Davon abgesehen entspricht es der schon in [10] verwendeten Vorgehensweise, die letztendlich eine Variante des geordneten Ditherings ist.
Basis des Ditherings ist die Zuordnung von individuellen Zufallswerten zu den Pixeln im Bildraum. Diese sind zwischen 0 und 1 gleichverteilt (Erwartungswert = 0,5) und werden von der ebenfalls zwischen 0 und 1 liegenden lokalen Intensität subtrahiert. Die Differenz x beider Werte wird mittels einer Stufenfunktion S(x) in den resultierenden lokalen Intensitätswert umgesetzt.
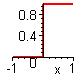
Verwendete Stufenfunktion
S(x)

Die ursprüngliche Intensität eines Farbverlaufs

1:1 den Pixeln zugeordnete Zufallswerte

Pixelweise ausgewertete Differenz
x

Nach Anwendung von
S(x)
Die Zuordnung der Zufallswerte erfolgt am geschicktesten durch eine Textur, deren Texel 1:1 auf entsprechende Pixel abgebildet werden und mit gleichverteilten Werten im Intervall [0..1] versehen sind. An den zur Erzeugung verwendeten Zufallsgenerator sind relativ geringe Anforderungen nötig, da durch die Texturwiederholung sich die Werte ohnehin entsprechend der Texturgröße wiederholen. Somit genügen schon einfache Modulo-Generatoren den Anforderungen. Wichtig ist jedoch, daß es sich tatsächlich um eine Gleichverteilung der Werte handelt, da nur so die Gleichheit von mittlerer Intensität nach dem Dithering und ursprünglicher Intensität garantiert ist. Eine solche Textur kann aus einer beliebigen Textur mit N Zufallswerten hergestellt werden, indem dem i-t größten Zufallswert der Wert I = (i - 1) / (N - 1) zugeordnet wird.
Verbesserung durch weichere Stufenfunktionen
Weil alle simulierten Pigmentflecken dieselbe Größe haben wirkt der auf diese Weise erzielte Verlauf ziemlich rauh. Betrachtet man nun den Pigmentauftrag stochastisch, so entspricht die Pigmentfleckengröße einer Zufallsdichte D(x) mit der gewählten Stufenfunktion als dazugehörigen Zufallsfunktion S(x). Die Differenz x wird hierbei als per x := 0.5*(x+1) auf das Intervall [0..1] abgebildet angenommen.
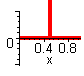
Dichte der Stufenfunktion:
dS(x)/dx
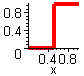
Stufenfunktion
S(x)
Ein besseres Ergebnis erhält man, indem man von einer Gleichverteilung zwischen einer kleinsten und einer größten Pigmentfleckengröße auf dem Papier ausgeht. Die dazugehörige Zufallsfunktion ist eine Verallgemeinerung der Stufenfunktion:
Slin(x) = Saturate(w * x + 0.5 * (1 - w))
und konvergiert für
w -> oo gegen diese.
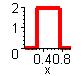
Dichte der Stufenfunktion (
w = 1/2):
dSlin(x)/dx
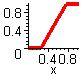
Stufenfunktion
Slin(x)

Nach Anwendung von
Slin(x)
Realistischer ist es jedoch, davon auszugehen daß schon die gesprühten Tropfen selbst einer Gleichverteilung unterliegen. Unter der Annahme, daß das Pigment noch flüssig bleibt und sich somit die bedeckte Fläche als Summe vieler Tropfengrößen ergibt, wird die Zufallsdichte bei längerem Sprühen zu einer Glockenkurve[14]. Ein qualitativ vergleichbares Ergebnis ergibt sich unter Annahme einer normalverteilten Zufallsdichte. Auch hier kann die Zufallsfunktion als verallgemeinerte Stufenfunktion gesehen werden.
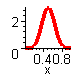
Dichte der Stufenfunktion (
w = 1/2):
dSlinsum(x)/dx
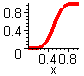
Stufenfunktion
Slinsum(x)

Nach Anwendung von
Slinsum(x)
Problematisch an den weicheren Stufenfunktionen ist, daß für Intensitätswerte am Rand des Intervalls [0..1] nach Sättigung im Rasterisierer nicht mehr der lineare Zusammenhang I = Mittelwert(S(x)) gilt. Insbesondere sind die Mittelwerte 0 und 1 nicht mehr möglich!
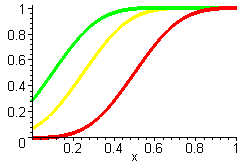
Darstellung von
Slinsum(x-Intensität) für Intensitäten von 0.5, 0.25 und 0.1
Beheben läßt sich dies, indem die Intensität von dem Intervall [0..1] auf das Intervall [- w/2 .. 1 + w/2] abgebildet wird. Danach sind Mittelwerte von 0 und 1 wieder möglich, es besteht aber weiterhin kein linearer Zusammenhang zwischen ursprünglicher Intensität und dem resultierenden Mittelwert mehr.
Ein adaptiver Korrekturansatz, bei dem die Breite der Stufenfunktion auf 2*min(Intensität,1-Intensität)/(max({Zufallswerte})-min({Zufallswerte})) beschränkt wird, stellt auch den linearen Zusammenhang wieder her. Allerdings erfolgt dies auf Kosten einer nicht mehr konstanten Streuverteilung, was allerdings nur bei weiten Verteilungen nachteilig ist.
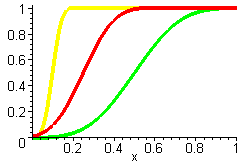
Darstellung von
Slinsum(x-Intensität) für dieselben Intensitäten nach passender Skalierung der Breite
Auf heutigen Bildschirmen ist die Bildauflösung um ein vielfaches geringer als die mit einem Airbrush minimal mögliche Pigmenttropfengröße. Es ist also zweckmäßig, von einer teilweise homogenen Pigmentverteilung auf den Pixeln auszugehen. Dies entspricht Zufallswerten gleichen Erwartungswerts, aber geringerer Varianz bei Bildung der Differenz x. Die Breite der Stufenfunktion kann zugleich zur Simulation unterschiedlich rauher Oberflächen herangezogen werden. Wird die Varianz darüber hinaus mit der Entfernung moduliert, erhält man den Effekt von mit zunehmender Entfernung schwächer werdender Details.
Bei geringerer Varianz überstreicht
x einen entsprechend kleineren Teil des Definitionsbereichs von
Slinsum(x-Intensität).
Je nach gewählter Breite der Stufenfunktion und Varianz der Zufallswerte ergeben sich somit Graphiken, die im Grenzfall bis hin zu photorealistischen Techniken oder Cartoonstil reichen.


Verschiedene Stufenfunktionsbreiten bei geringer Varianz
Verwendung der gewonnenen Intensitätsverteilung
Die im Airbrush eingesetzten Pigmente mischen sich meist deckend oder subtraktiv, während in der Computergraphik eine additive Farbmischung bevorzugt wird. Da hier nur der resultierende Farbauftrag, nicht aber sein Zustandekommen modelliert wird, stellt dies keine Einschränkung dar. Es ist allerdings darauf zu achten, daß die beschriebene Modellierung stets nur skalare Werte liefern kann. Somit muß bei der Beleuchtungsberechnung als Erstes die skalare Intensität der einzelnen Beleuchtungskomponenten ermittelt und auf diesen getrennt der Sprühvorgang angewendet werden. Erst dann können die so erhaltenen lokalen Intensitäten mit den dazugehörigen Farbwerten multipliziert und aufsummiert werden. Andernfalls würden sich innerhalb ein- und desselben simulierten Pigmentauftrags unterschiedliche Farbwerte ergeben.
Animationsfähigkeit
Bildraumbasierte Verfahren haben meist den Nachteil, daß bei bewegten Objekten die Abhängigkeit des Verfahrens von der Position im Bildraum sichtbar wird. Der Effekt ähnelt der Betrachtung durch eine angerauhte Glasscheibe und wird auch als "Shower Door Effect" bezeichnet[12]. Um ihn zu vermeiden, wird jedes Objekt mit einer Modulationstextur versehen, welche kontinuierliche, richtungsunabhängige Verläufe zwischen 0 und 1 verhält. Derartige Texturen können z.B. durch stark gefilterte Perlin-Noise-Texturen oder überlagerte Sinusfunktionen realisiert werden. Der Wert dieser Textur an einem Punkt wird zu dem Zufallswert im Bildraum modulo 1 hinzuaddiert:
Zufallswert_animiert = frac(Zufallswert + Modulationswert)
Auf diese Weise ändert der Pigmentierungsgrad eines Pixels, die Stärke der Änderung ist dabei direkt vom Ausmaß der Objektbewegung abhängig und vermittelt den Eindruck, als ob das Bild mit dem Airbrush überarbeitet werden würde. Als angenehmen Nebeneffekt verringern sich auch die Regelmäßigkeiten, welche durch die Wiederholung der Zufallstextur entstehen.

Würfel mit Modulationstextur auf der Oberfläche

Sprüheffekt mit Modulation auf einem rein ambient beleuchteten Würfel

Derselbe Würfel, leicht gedreht

Die Differenz beider Bilder verdeutlicht die Auswirkung auf animierte Bilder
Die Texturkoordinaten für die Modulationstextur können oftmals direkt aus bestehenden Texturkoordinaten eines Objekts übernommen werden. Andernfalls können geeignete Koordinaten durch Betrachtung des an der Objektoberfläche gespiegelten Sichtvektors eines im Objektraum positionierten Betrachters gewonnen werden. Hierbei treten zwar an Kanten Sprünge in den Texturkoordinaten auf, die aber ohnehin durch die Intensitätssprünge in der Beleuchtung des Objekts überdeckt werden.
Kritischer ist jedoch, daß bei sehr kleinen Sichtwinkeln auch die Änderung der resultierenden Texturkoordinaten pro Pixel sehr klein wird und in Folge die Effektivität der Modulation sinkt. In diesen Fällen sollte die Auflösung der Modulationstextur dynamisch als Funktion der Texturkoordinatenänderung pro Pixel erhöht werden.

Modulationstextur nach Zoom auf eine Ecke des obigen Würfels

Dieselbe Szene mit dynamisch angepaßten Modulationstexturkoordinaten
Nachbildung von Schraffurlinien
Polierte und gebürstete Oberflächen werden im Airbrush häufig durch feine Linienstücke in Bearbeitungsrichtung dargestellt. Die Richtung der Linien kann als 2D-Vektoren auf der Oberfläche spezifiziert werden, welche anschließend in die ebenfalls zweidimensionale Bildebene projiziert werden. Die Darstellung der Linien ist somit nichts anderes als die Visualisierung eines 2D-Vektorfelds, wobei das Aussehen nur von Richtung der Linien und der Bildauflösung abhängen soll, nicht aber von Lage, Betrag oder Vorzeichen der Vektoren.
Ein geeignetes Verfahren stellt das LIC(Line Integral Convolution)-Verfahren dar, bei dem ein symmetrischer eindimensionaler Filterkern auf eine zweidimensionale Zufallstextur angewendet wird (man vergleiche auch mit [11]). Als Orientierung des eindimensionalen Filters in der zweidimensionalen Ebene wird dabei der jeweils lokal darzustellende Vektor verwendet[13].
Als Ausgangstextur wird die schon für die Intensitätsstreuung verwendete Zufallstextur verwendet. Um den Filter möglichst effizient zu realisieren, sollte einerseits jeder Abtastpunkt einen anderen Zufallswert ermitteln, andererseits sollte der Filterkern auf das keinstmögliche Umfeld eines Abtastpunktes beschränkt sein. Der größtmöglichste Abstand zweier Pixel tritt entlang der Diagonalen auf und beträgt somit sqrt(2) * Pixelgröße.
Leider ergibt die Summe i´ mehrerer gleichverteiler Zufallswerte i keinen gleichverteilten Zufallswert mehr. Stattdessen ergibt sich für die ungewichtete Summe aus n gleichverteilten Zufallswerten mit Werten zwischen 0 und 1 folgende Zufallsdichte[14]:
D(i´) = 1 / (2 * (n - 1)!) * Summe(k = 0..n, (-1)k * (nk) * (i´ - k)(n - 1) * sign(i´ - k))
Gleichverteilte Werte i erhält man, indem man die dazugehörige Zufallsfunktion S(i´) heranzieht: i = S(i´). Für eine feste Anzahl von Abtastpunkten kann diese vorberechnet und in einer Textur für das Intervall [0..n] abgelegt werden. Die so gewonnenen Werte werden wie bei dem schon beschriebenen Verfahren eingesetzt.

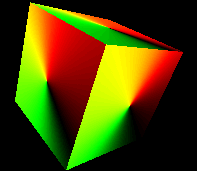
Farbcodierte Vektoren
(r,g,b) = ((x,y,z,)+1)/2 in Welt- und in Bildkordinaten

Errechnete Schraffur
Einen kontinuierlichem Übergang zwischen Zufallspunkten und Zufallslinien ist durch lineare Interpolation beider Techniken möglich. Dasselbe Ergebnis wäre zwar auch über eine entsprechend stärkere Gewichtung des mittleren Filterpunktes möglich, würde aber zugleich die Gestalt von S(i´) von der Gewichtung abhängig machen.
Wahl eines geeigneten Beleuchtungsmodells
Prinzipiell ist für den Airbrusheffekt jedes Beleuchtungsmodell geeignet, solange es sich in einen Ambient-Diffusen und einen spekularen Term zerlegen läßt und für den spekularen Term reflektierte Sichtvektoren berechnen kann. Die Verteilung dieser Vektoren soll dabei deren Anteil an der spekularen Reflexion entsprechen. Aufgrund der geringen Eindringtiefe genügt die Betrachtung der Strahlenoptik für nahezu alle im Alltag vorkommenden Metalloberflächen.
Im Folgenden wird eine Variante des Phong-Modells vorgestellt, welches an das von Ashikmin und Shirley in [15] präsentierte Modell angelehnt ist und einen guten Kompromiß aus erzielter Qualität zu aufzuwendender Leistung und leichter Handhabbarkeit darstellt. Ebenso wie dieses setzt es sich aus einem spekularen und einem diffusem Term zusammen und unterstützt sowohl einen winkelabhängigen Fresnelterm zur Farbkorrektur als auch die Nachbildung anisotroper Oberflächen, verwendet aber einen einfacheren Term für diffuse Reflexionen. Darüber hinaus wird es für den Einsatz in einer rein lokalen Beleuchtungsberechnung zusätzlich um einen ambienten Term sowie eine Environmentmap ergänzt.
Diffuser Anteil
Der diffuse Anteil berücksichtigt den durch Mehrfachreflexion an Mikrofacetten der Oberfläche in beliebige Richtungen gestreuten Anteil des Lichts. Er setzt sich aus einem Lambertschen Term für gerichtet einfallendes Licht sowie einem konstanten Term für aus der Umgebung einfallendes Licht zusammen:
DiffusesLicht = DiffuseFarbe * (Summe(Lichtquellen, cos(Einfallswinkel) * LichtintensitätLichtquelle(cos(Einfallswinkel))) + LichtintensitätAmbient)
Im klassischen Lambertschen Modell ist LichtintensitätLichtquelle(cos(Einfallswinkel)) für positive cos(Einfallswinkel) eine positive Konstante und ansonsten gleich 0. Es bietet sich aber an, hier ähnlich dem Cool-to-Warm-Shading mit einem Gegenlicht (mit positivem oder negativen Vorzeichen) zu arbeiten, um den plastischen Eindruck zu erhöhen[16]. Somit wird LichtintensitätLichtquelle(cos(Einfallswinkel)) = LichtintensitätLichtquelle für cos(Einfallswinkel) > 0 und ansonsten gleich der Lichtintensität des Gegenlichts.
Für die DiffuseFarbe gilt aufgrund von Mehrfachreflexion:
DiffuseFarbe ~ Mittelwert(SpekulareFarbeAnzahlReflektionen) * AnteilMehrfachreflexionen
und ist somit je nach Oberflächenbeschaffenheit wesentlich schwächer und stärker gefärbt als die spekulare Farbe. Bei Verwendung von Gegenlichtern sollte zudem die ambiente Intensität angepaßt werden, um die Änderung der Gesamthelligkeit durch das Gegenlicht zu kompensieren. Aufgrund der geringen Intensität des diffusen Anteils kann für Renderingzwecke auf die Berücksichtigung des Fresnelterms sowie Abschwächung bei hoher spekularer Reflexionsintensität aufgrund der Energieerhaltung verzichtet werden.
Spekularer Anteil
Der Spekulare Anteil wird nach dem Phong oder dem Blinn-Phong-Modell berechnet:
SpekularesLicht = SpekulareFarbe * (Summe(Lichtquellen, Saturate(cos(Spekularwinkel))Spekularexponent * c * LichtintensitätLichtquelle))
Im Phong-Modell ist der Spekularwinkel gleich dem Winkel zwischen Sichtstrahl und dem reflektiertem Lichtstrahl, welcher mit dem Winkel zwischen einfallendem Licht und reflektierten Sichtvektor identisch ist. Besser geeignet [18], aber für jede Lichtquelle getrennt zu berechnen, ist der Spekularwinkel als Winkel zwischen dem Halfway-Vektor und der Oberflächennormale, wie er im Blinn-Phong-Modell verwendet wird.
Dies liegt in der physikalischen Bedeutung des Halfway-Vektors: Dieser gibt die Normale einer unter den gegebenen Licht- und Sichtrichtungen perfekt reflektierenden Oberfläche an. Betrachtet man nun eine aus Mikrofacetten bestehende Oberfläche mit dem Spekularexponenten als Maß für deren Glattheit, so gibt der Term cos(Spekularwinkel)Spekularexponent mit dem Normalisierungsfaktor c für die Energieerhaltung den Anteil der reflektierenden Mikrofacetten an der Gesamtoberfläche an. Im Gegensatz dazu verfügt das normale Phong-Modell über keine direkte Interpretation für eine aus Mikrofacetten zusammengesetzte Oberfläche.
Die spekulare Farbe entspricht direkt der Farbe des vom Metall reflektierten weißen Lichts und kann für unpolarisiertes Licht als Mittelwert der Fresnelterme für polarisiertes Licht bei entsprechender Frequenz berechnet werden. Der Normalisierungsfaktor c ergibt sich zu c = (Spekularexponent + 1) / (2 * Pi) und kann mit der spekularen Farbe vormultipliziert werden, so daß hierfür keine gesonderte Konstante nötig ist.
Im BRDF-Modell von Ashikmin und Shirley wird der Korrekturfaktor c noch mit 1/max(Lichtvektor.Normale,Sichtvektor.Normale) multipliziert. Dieser kann aber bei ohnehin rein lokaler Beleuchtungsberechnung wie im Blinn-Phong-Modell durch den nicht-reziproken Term 1/Lichtvektor.Normale ersetzt werden, welcher bei Anwendung der BRDF durch den ebensogroßen Faktor für einfallendes Licht kompensiert wird und somit entfällt.
Environment Mapping
Für die Nachbildung von Spiegelungen wird das einfallende Licht einer Environment Map entnommen. Um verschieden rauhe Oberflächen zu simulieren wird dazu der reflektierte Sichtvektor mit zufälligen Vektoren so moduliert, daß der endgültige Reflexionsvektor derselben Verteilung folgt wie der Intensitätsverlauf eines spekular reflektierten Lichtes aus derselben Richtung. Hierbei genügt es, nur ein einzigen Wert pro Pixel aus der Environmentmap auszulesen, da das dadurch erzeugte Muster sich optisch kaum von der Streuung des simulierten Airbrushes unterscheidet. Vorraussetzung dazu ist allerdings eine ausreichend tiefpaßgefilterte Environment Map, da starke Änderungen der Farbe innerhalb eines Winkels in Größenordnung des Streukegels des modulierten Reflexionsvektors zu einem unruhigen Gesamtbild führen würden.
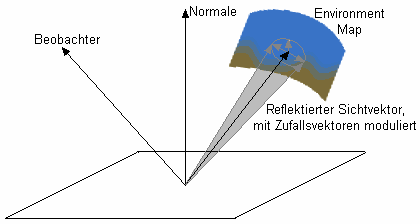
Die einfachste Realisierung einer passenden Environment Map stellen CubeMaps dar. Allerdings ist die Generierung solcher Environment Maps vergleichsweise umständlich. Da sich eine stark vereinfachte Umgebung als Kombination je einer einfarbigen Boden- und Himmelshemisphäre deuten läßt, bietet es sich an, den polaren Winkel der Reflexionsrichtung zu verwenden, um zwischen der Farbe des Himmels und der des Bodens zu interpolieren. Um mehr Variation zu erhalten, kann in Horizontnähe die Farbe zusätzlich in Abhängigkeit vom azimuthalen Winkel variiert werden. Eine besonders für stark glänzende Oberflächen interessante Variation bietet sich, wenn man dazu eine gewöhnliche, zweidimensionale Textur verwendet, welche z.B. einem Panoramaphoto entstammen kann. Damit ergibt sich für das Aussehen der Environmentmap ein Zylinder, dessen Mantel die 2D-Textur bildet und desen Ober- und Unterseiten der Himmels- bzw. Bodenfarbe entsprechen. Für die Koordinaten der Textur ergeben sich somit u = 1/2 + arctan(x / z) / (2 * Pi) und v = 1/2 * (y / sqrt(1 - y2))/h für einen normalisierten reflektierten Vektor (x,y,z) und Texturkordinaten u,v innerhalb [0..1] auf der Mantelfläche sowie v außerhalb [0..1] für die Ober- und Unterseite.
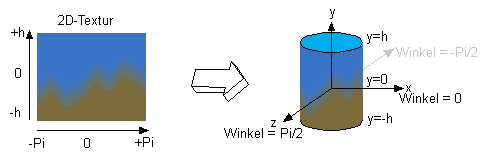
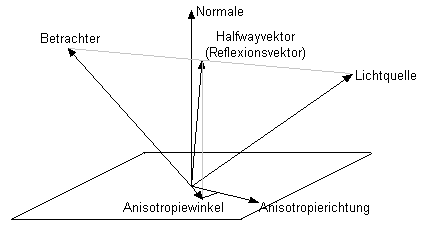
Anisotropie
Einfache Anisotropie einer Oberfläche kann als Richtung maximaler Rauhigkeit mit senkrecht dazu liegender Richtung minimaler Rauhigkeit modelliert werden[15]. Der dazugehörige Spekularexponent ergibt sich als lineare Interpolation zwischen einem minimalen und einem maximalen Spekularexponenten in Abhängigkeit des Winkels zwischen dem auf die Oberfläche projizierten Halfwayvektor und der Anisotropierichtung der Oberflächenebene:
Spekularexponent = SpekularexponentMin * Orientierung + SpekularexponentMax * (1 - Orientierung))
mit
Orientierung = cos(Anisotropiewinkel)2 = ((Halfwayvektor.Anisotropieachse)2) / (1 - (Halfwayvektor.Normale)2)
Auch hier gibt es eine anschauliche physikalische Interpretation, indem man analog zum isotropen Blinn-Phong-Modell den Halfwayvektor als Normale einer reflektierenden Mikrofacette nimmt. Die Verteilung der Mikrofacettennormalen hängt jetzt allerdings auch von deren Richtung parallel zur Oberfläche ab, und entsprechend wird auch der Spekularexponent als Maß der Glattheit zu einer Funktion der Orientierung des Halfwayvektors parallel zur Oberfläche.
Die Normalisierungskonstante c kann auch hier wieder vorberechnet werden und ergibt sich zu: c = sqrt((SpekularexponentMin + 1) * (SpekularexponentMax + 1)) / (2 * Pi)
Ein Spezialfall anisotroper Oberflächen sind Kanten: An diesen verteilen sich die Oberflächennormalen im gesamten Bereich zwischen den Normalen der angrenzenden Seiten. Somit können durch Linien mit entsprechend niedrigeren Spekularexponenten für senkrecht zur Kante einfallendes Licht die meist vernachlässigten Reflexionen an Kanten nachgebildet werden. Als Normale der Kante wird
der Mittelwert der angrenzenden Seitennormalen verwendet.


Würfel ohne und mit nachgezeichneten Kanten
An für sich sollte auch die Verteilung des reflektierten Sichtvektors für Spiegelungen von der Anisotropie beeinflußt werden. Allerdings ist die Auflösung mit nur einem Abtastwert pro Pixel und vorgefilterter Environmentmap in der Praxis so grob, daß die Auswirkungen der Anisotropie kaum sichtbar sind und somit vernachlässigt werden können. Auch bei Airbrusharbeiten werden anisotrope Effekte üblicherweise nur über die Verteilung der hellsten Lichtreflexe imitiert.
Bumpmaps
Nachdem mit der Normalen und der dazu orthogonalen Anisotropierichtungsebene ein fertiges karthesisches Koordinatensystem im Tangentialraum festgelegt ist liegt es nahe, dieses auch für Änderungen der Oberflächennormale zur Simulation von Unebenheiten auf Pixelebene zu verwenden. Als geeignete Bumpmap-Verfahren bieten sich insbesondere Offset Maps (Textur enthält einen Vektor, der zur Oberflächennormale hinzuaddiert wird) und Rotation Maps (Textur beschreibt Drehung der Oberflächennormale) an[17]. Die durch Filterung bei Texturverkleinerung verschwindenden Unterschiede der Normalen können dabei nicht nur in einem entsprechend angepaßten Spekularexponenten aufgefangen werden[18,19], sondern auch durch entsprechende Änderung der Varianz der Zufallswerte weiter zur Darstellung einer unebenen Oberfläche im Airbrushstil verwendet werden. Geeignet sind Bumpmaps vor allem für Normalenänderungen niedriger Amplitude und Frequenz, da signifikante Änderungen in der Höhe im Airbrush besser durch direkte Nachbildung über präzise Techniken wie Masken wiedergegeben werden, während kleinräumige Strukturen direkt durch die Art des Pigmentauftrags simuliert werden. Als generelle Grenzen von Bumpmaps treten zudem bei großen Amplituden und flachen Betrachtungswinkel der flache Texturcharakter unangenehm in Erscheinung, wohingegen sich feine Texturdetails bei Texturfilterung schnell gegenseitig aufheben.
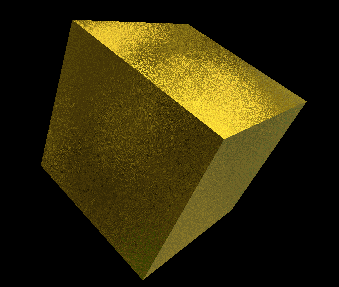

Würfel mit ebener und unebener Oberfläche via Bumpmap
Erweiterte Lichteffekte
Glanzlichter
Reflexionen, die den gewählten Dynamikbereich überschreiten, strahlen in ihre Umgebung aus. Zur Nachbildung dieses Effekts wird ein an HDR-Rendering[20] angelehntes Verfahren mit zwei Durchgängen angewendet:
Im ersten Schritt wird eine Textur erstellt, die nur die Lichtintensität der spekularen Beleuchtungskomponente des Bildes enthält. Diese kann je nach Stärke der Überstrahlung mit einem multiplikativen Faktor moduliert sein.
Im zweiten Schritt werden im Bildraum die gefilterten Werte aus der spekularen Textur ausgelesen und in weißer Farbe additiv dargestellt. Zur vereinfachten Nachbildung des Sprüheffektes genügt es, je nach Position im Bildraum einige exemplarische Werte innerhalb des Filterkerns zu entnehmen, so daß kein vollständiger und aufwendiger Filterkern nötig ist. Die Lesepositionen X_t aus der spekularen Textur kann ggf. um den Betrag b in Richtung des Lichtes (in Bildebene projiziert) verschoben sein und ergibt sich für den Pixel am Ort X_p im i-ten Durchgang zu:
X_t = X_p + 2D-Zufallsvektor(i,X_p) + b * Lichtrichtung
Sterneffekte
Sternförmige Lichtreflexe könnten zwar ebenfalls in einem zweiten Durchgang durch Filterung aus der spekularen Textur gewonnen werden, erfordern aber einen in der Praxis nicht vertretbaren Rechenaufwand. Sinnvoller ist es, die spekulare Textur nur an einigen exemplarischen Punkten auszuwerten und entsprechend der aufgefundenen Intensität die sternförmigen Effekte zu platzieren. Zu beachten ist, daß alle Sterne dieselbe Orientierung und Gestalt haben, einzig die Helligkeit und Größe darf variieren.
Passende Testpunkte können als 3D-Vertices von Hand den zu zeichnenden Objekten hinzugefügt werden, oder sie können direkt als zufällige Auswahl aus den bestehenden Vertices eines Objekts entnommen werden. Angezeigt werden sie idealerweise als Billboards bzw. Pointsprites.
Implementierung
Verwendete API-Bestandteile
Realisiert wurde das beschriebene Verfahren in Direct3D 9 mit 2.0x-Shadern. Diese sind die Minimalanforderung, um das gesamte Rendering (bis auf die zusätzlichen Effekte) in einem einzigen Pass zu erledigen und sind auf praktisch allen aktuellen Standardgraphikkarten verfügbar.
Die gesamte Beleuchtungsberechnung findet aufgrund der zu erwartenden hohen Spekularexponenten komplett im Pixelshader statt. Ein dazugehöriger Vertexshader ist dennoch nötig, um die lokalen Parameter an diesen übergeben zu können. Davon abgesehen entspricht er praktisch der Standardfunktionalität der fest vorgegebenen Graphikpipeline von DirectX 9. Im Pixelshader sind prinzipiell beliebig viele Lichtquellen möglich, deren Parameter denen der vorgegebenen Lichtquellen in D3D 9 entsprechen.
Der Dithervorgang zur Sprühsimulation ist streng genommen nur für einen linearen Zusammenhang zwischen berechneter Farbintensität und auf dem Bildschirm sichtbarer Helligkeit korrekt. Andernfalls müssen die Werte per Gammakorrektur konvertiert werden. In D3D 9 wird aber innerhalb der Shader ein linearer Zusammenhang vorausgesetzt[21], so daß keine weiteren Vorkehrungen hierzu nötig sind.
VertexShader
Im Vertexshader werden sämtliche Vektoren in Weltkoordinaten transformiert, so daß im Pixelshader keine weiteren Transformationen für die dort hinzukommende EnvironmentMap und die Lichtquellen mehr nötig sind. Zu beachten ist, daß die Koordinaten für die Zufallstextur im Bildraum schon hier vorberechnet werden (abgesehen von der perspektivischen Division), da in 2.0x-Pixelshadern kein Zugriff auf die Position eines Pixels möglich ist. Falls nötig, werden geeignete Koordinaten für die Modulationstextur ebenfalls generiert. Das Flag LOCALVIEWER verhält sich wie der D3D-Renderstatus D3DRS_LOCALVIEWER und ist nicht nur für orthogonale Projektion sinnvoll, sondern kann auch durch einen übergroßen Sichtwinkel entstehende Effekte vermeiden.
PixelShader
Im Pixelshader erfolgt die komplette Beleuchtungsberechnung. Hier sind 2.0a bzw. 2.0b-Shader im Vorteil, da sie durch eingebaute Kontrollstrukturen sowie höherer Zahl an erlaubten Anweisungen eine unterschiedliche Zahl an Lichtquellen ohne Neuübersetzung des Shaders und in einem Durchgang unterstützen. Der Shader im Detail:
Parameter für Lichtquellen und Umgebungslicht
In der Struktur Lichtquelle werden die Parameter einer jeden Lichtquelle abgelegt, wobei die Werte Ambient, Diffus, Spekular, Typ und Vektor weitgehend denen der vordefinierten Standard-D3D-Lichtquellen entsprechen und um eine Gegenlichtfarbe GegenlichtDiffus ergänzt werden. Sämtliche Farbwerte liegen als RGBA-Farben vor. Im Gegensatz zu D3D werden Spotlights und entfernungsabhängige Abschwächung nicht unterstützt, können aber durch Erweiterung des Shaders mit berücksichtigt werden.
Zusätzlich kann eine einzelne Environment Map im RGBA-Format verwendet werden, deren Farbwert mit LichtfarbeEnv multipliziert wird, um die Farbe der Umgebung dynamisch anpassen zu können. Die richtungsabhängige Farbe aus der Environment Map wird über die Funktion EnvFarbe() ausgelesen. Für diese Funktion gibt es mehrere Möglichkeiten. Am einfachsten zu implementieren ist die Verwendung vorberechneter CubeMaps, gespeichert in der Textur EnvMap:
float4 Envmap_Cube(float3 Richtung)
{
return texCUBE(EnvMap,Richtung);
}
Eine andere Variante verzichtet auf Texturen und berechnet anhand einiger Parameter eine einfache Umgebung. Benötigt werden als benutzerdefinierte Parameter die beiden Farbwerte, die gewünschten Position des Horizonts relativ zur y-Komponente eines normalisierten Richtungsvektors und als Eingabe einen normalisierten Richtungsvektor. Über eine Summe mehrere Sinusfunktionen, skaliert mit dem Parameter Horizontvarianz, wird die Höhe zusätzlich zur Imitation einer einfachen Landschaft moduliert. Die Schärfe des Boden-Himmel-Farbübergangs wird über Horizontverlauf eingestellt:
//Parameter
float4 HorizontfarbeOben; //RGB-Farbe des Himmels
float4 HorizontfarbeUnten; //RGB-Farbe des Bodens
float Horizonthoehe;
float Horizontverlauf;
float Horizontvarianz;
float4 EnvmapParamHorizont(float3 Richtung)
{
//ein möglicher Horizontverlauf auf Basis von Sinusfunktionen
float Horizontstruktur = Horizontvarianz * ( 0.2 * sin(5 * Richtung.x * PI)
+ 0.5 * cos(3 * Richtung.x * PI)
+ 1 * sin(1 * Richtung.x * PI));
//interpoliert zwischen 2 Farben
float Horizontposition = 0.5 - (0.5 * (Richtung.y + 1)-Horizonthoehe)*Horizontverlauf;
float Farbmischung = saturate(Horizontposition+Horizontstruktur);
return lerp(HorizontfarbeOben,HorizontfarbeUnten,Farbmischung);
}
Die beschriebene zylindrische Environment Map erlaubt es, bestehende (Panorama-)Bilder als Environmentmap zu verwenden. Die Pixel am oberen und am unteren Bildrand sollten jeweils in einer Farbe vorliegen, da diese auch für die Ober- und Unterseite des Zylinders mittels Clamp-Adressmodus verwendet werden. Um eine lückenlose Interpolation am Rand der Textur zu ermöglichen sollte für die horizontale Texturkoordinate Wraparound verwendet werden. Mit einem normalisierten Richtungsvektor als Eingabe liefert folgende Funktion den passenden Farbwert:
//Parameter
float XzuY; //Seitenverhältnis der eingesetzten Textur
float4 Envmap_Zylinder(float3 Richtung)
{
//zylindrische Textur, Breite:Höhe = 2:1
//Addressmodi: x=wrap, y=clamp
float2 TexKoord;
TexKoord.x = 1 - (atan2(Richtung.x,Richtung.z) / (2 * PI));
TexKoord.y = 0.5 * (1 - XzuY * Richtung.y / sqrt((1 - Richtung.y * Richtung.y)));
return tex2D(EnvMap,TexKoord);
}
Das zylindrische Mapping läßt sich vereinfachen, wenn die Ausgangstextur nur eine Hälfte des Zylinders abdeckt und für die andere Hälfte gespiegelt wird. Verwendet man eine passend vorverzerrte Textur, genügt für das Auslesen der Environment Map folgende einfache Funktion:
float4 Envmap_Halbzylinder(float3 Richtung)
{
//Addressmodi: x=mirror, y=clamp
float2 TexKoord = 0.5 * (1 + Richtung);
return tex2D(EnvMap,TexKoord);
}
Dazugehöriger Shader zum Erzeugen einer passend vorverzerrten Textur als Rendertarget:
const float PI=3.14159265359;
sampler envmap;
float XzuY; //Seitenverhältnis der eingesetzten Textur
float4 Halbzylindertextur(float2 Texpos : TEXCOORD0 ) : COLOR
{
//Achtung: Eingabeposition in Rendertargetkoordinaten liegt in [-1..1]^2, nicht [0..1]^2 !
//berechne z-Komponente des Richtungsvektors anhand der Texturkoordinaten der verzerrten Textur
//(Richtungsvektor ist dabei nicht normalisiert)
float Texposz=sqrt(1 - Texpos.x * Texpos.x);
//berechne halbzylindrisches Mapping
float2 envmap_uv;
envmap_uv.x = (atan2(Texpos.x,Texposz)/PI) + 0.5;
//halbe Höhe aufgrund Spiegelung der Ausgangstextur:
envmap_uv.y = 0.5 * (1 + 0.5 * XzuY * Texpos.y / sqrt((1 - Texpos.y * Texpos.y)));
return tex2D(envmap,envmap_uv);
}
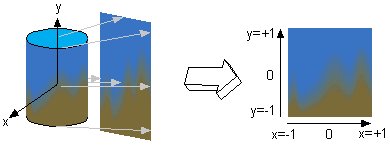
Erweiterte Shader, mit der auch Bilder ohne konstante Farbe am oberen und unteren Rand verwendet werden können, finden sich im Anhang.
Parameter des Materials
Die Farbwerte SpekulareFarbe für einfach und DiffuseFarbe für mehrfach reflektiertes Licht ergeben sich direkt aus der nachzubildenden Metalloberfläche, der Spekularexponent wird entsprechend dem Blinn-Phong-Modell der Oberflächenrauhigkeit angepaßt.
Um die interaktive Handhabung zu vereinfachen berechnen sich die anisotropen Spekularexponenten zu Spekularexponent/Isotropie sowie Spekularexponent*Isotropie, ein Wert von 1 für Isotropie ergibt somit eine isotrop reflektierende Oberfläche. Um auch komplexere Anisotropiestrukturen darzustellen kann der Tangentenvektor mittels einer Anisotropietextur in der Ebene gedreht werden. Die Textur speichert dabei direkt den Wert der gedrehten Tangente, ausgedrückt im zweidimensionalen Tangente-Binormale-Koordinatensystem.
Als Bumpmap wird eine Offset Map verwendet, so daß die zum Variieren der Normale verwendeten Offsetvektoren in derselben zweidimensionalen Form wie die gedrehten Tangentenvektoren der Anisotropie gespeichert werden können. Weil alle Offsetvektoren somit in der Oberflächenebene liegen, sind die resultierende Normalen nicht mehr normalisiert. Dies ist allerdings kein Nachteil, da aufgrund der metalltypisch hohen Spekularexponenten sowieso normalisiert werden sollte, um Interpolationsartefakte der Bumpmap zu vermeiden. Der zweite Nachteil von derartigen Offsetmaps, der eingeschränkte Bereich resultierender Vektoren (maximal 45 Grad Abweichung zur ursprünglichen Normalen bei Offsetwerten innerhalb [-1..1] in Tangenten- bzw. Binormalenrichtung) ist ebenfalls unkritisch: Dies reicht selbst für bei Wellblech oder Riffelblech üblichen Werten aus, größere Abweichungen sind aus schon genannten Gründen ohnehin nicht empfehlenswert. Sowohl bei der Anisotropie- als auch der Bumpmap ist darauf zu achten, daß sich bei Texturwiederholung die
Vektoren durch Interpolation an den Kanten gegenseitig aufheben können.
Parameter des Sprüheffekts
Die Parameter Streuung und Verlauf beeinflußen Varianz der Zufallswerte und die Breite der Stufenfunktion bei Berechnung der lokalen Intensität. Für den Einsatz im Environmentmapping und den Glanzlichtern enthält die Zufallstextur pro Texel gleich 4 verschiedene Zufallswerte. Für die Modulationstextur genügt dagegen ein Wert pro Texel. Über die z_Daempfung kann die Abnahme der Varianz in Abhängigkeit von der z-Position des gerenderten Objekts variiert werden, um eine entfernungsbedingte Abnahme an sichtbaren Details nachzubilden.
Als Anzahl der Abtastpunkte für den Sprüheffekt hat sich in der Praxis ein Wert von 5 als Minimum für einen gut sichtbaren Effekt herausgestellt. Mehr Abtastpunkte verbessern die Qualität, führen aber schnell zu Engpässen bei der Übersetzung von 2.0/2.0a-Shadern mangels dynamischer Flußkontrolle bei zugleich stark begrenzter Länge. Die Relinearisierer-1D-Textur dient zur Wiederherstellung gleichverteilter Zufallswerte nach Anwendung des Schraffurfilters.
Für die Sprühfunktion Spray(Intensitaet,Spruehparameter) selbst gibt es mehrere Möglichkeiten. Die einfachste ist mit konstanter Korrektur und linearem Verlauf zwischen 0 und 1:
float Spray(float Intensitaet, float Spruehparameter)
{
float LokaleIntensitaet = Intensitaet - Spruehparameter;
float Korrektur = 1 - Streuung;
return saturate((LokaleIntensitaet - 0.5) / Verlauf * Korrektur + 0.5);
}
Dieselbe Funktion mit adaptiver Korrektur:
float Spray(float Intensitaet, float Spruehparameter)
{
float LokaleIntensitaet = Intensitaet-Spruehparameter;
float Korrektur = 2 * saturate(min(Intensitaet,1 - Intensitaet)) * (1 - Streuung);
return saturate(0.5 + ((LokaleIntensitaet - 0.5) / (Verlauf * Korrektur)));
}
Die bei Annahme mehrerer Schichten aus gleichverteilten Sprühtropfen entstehende S-Kurve als Zufallsfunktion läßt sich näherungsweise über die in der Shadersprache schon enthaltene Smoothstep-Funktion darstellen. Bei dieser handelt sich dabei praktisch um eine Hermite-Interpolation, welche einen Eingabewert x auf das Interval [a..b] begrenzt und anschließend den Wert Smoothstep(a,b,x) = 3 * y2 - 2 * y3 mit y = (x - a) / (b - a) zurückgibt. Die entsprechenden Varianten für konstante und adaptive Korrektur sind damit:
float Spray(float Intensitaet, float Spruehparameter)
{
//konstante Korrektur
float LokaleIntensitaet = Intensitaet-Spruehparameter;
float Korrektur = 1 - Streuung;
return smoothstep(-Verlauf * Korrektur,Verlauf * Korrektur,2 * (LokaleIntensitaet - 0.5));
}
float Spray(float Intensitaet, float Spruehparameter)
{
//adaptive Korrektur
float LokaleIntensitaet = Intensitaet - Spruehparameter;
float Korrektur = 2 * saturate(min(Intensitaet,1 - Intensitaet)) * (1 - Streuung);
return smoothstep(-Verlauf * Korrektur,Verlauf * Korrektur,LokaleIntensitaet - 0.5);
}
Vorbereitung interpolierter Werte
Zuerst werden die auf Vertexbasis interpolierten Werte TexNormale, Tangente, Binormale, Textur (Texturkoordinaten) und TexturMod (Modulationstexturkoordinaten) vorbereitet und ggf. normalisiert. Anschließend werden die Bump- sowie Anisotropietexturen ausgewertet und die Anisotropietangente in Bildkoordinaten vorbereitet:
//BumpMap
float2 Offset = tex2D(BumpMap,Textur);
float3 Normale = normalize(TexNormale + Offset.x * Tangente + Offset.y * Binormale);
//Anisotropiehauptachse (Tangente der Schraffur)
float2 Rotation = normalize(tex2D(AnisoMap,Textur).xy);
float3 Anisotropieachse = Rotation.x * Tangente + Rotation.y * Binormale;
//Anisotropietangente projiziert und skaliert
float3 Anisotropietangente = mul(matViewProjection,float4(Anisotropieachse.xyz,0));
float2 AnisotropietangenteBild = 1 / (TexGroesse / sqrt(2))
* normalize(Anisotropietangente.xy
- Anisotropieachse.z * normalize(BildPosition.xy));
Berechnung und Modulation des Sprühparameters
Für die Variation des Sprüheffekts wird der Z-Wert des Pixels verwendet: LokaleStreuung = Streuung * (1 - (BildPosition.z / BildPosition.w) * z_Daempfung) Dieser muß, ebenso wie die Koordinaten TexPos für die Position des Pixels im Bildraum, noch perspektivisch dividiert werden. Der entsprechende Zufallswert eines Pixels wird anschließend mit dem Wert ZufallswertAniso aus dem LIC-Verfahren gemischt. Letzterer ergibt sich als relinearisierte Summe über die benachbarten Zufallswerte in Richtung der projizierten Anisotropietangente:
//berechne linear gefilterten Wert
float4 ZufallswertAniso = Zufallswert;
for(int i=0; i<((Abtastpunkte - 1) / 2); i++)
{
TexPosP-= AnisotropietangenteBild;
TexPosN+= AnisotropietangenteBild;
ZufallswertAniso+= tex2D(Zufallswerte,TexPosP);
ZufallswertAniso+= tex2D(Zufallswerte,TexPosN);
}
//erzeuge gleichverteilte Werte:
ZufallswertAniso = tex2D(Relinearisierer,ZufallswertAniso / Abtastpunkte);
//Mische Schraffur mit normalem Zufallswert:
Zufallswert = lerp(ZufallswertAniso,Zufallswert,Isotropie);
Der fertige Sprühparameter eines Pixels berechnet sich dann zu float4 Spruehparameter = LokaleStreuung * (0.5 - frac(Modulation+Zufallswert));.
Um zu verhindern, daß die Modulationstextur bei starker Skalierung ineffizient wird kann man Mipmapping einsetzen, wobei die größte Mipmap so gewählt wird, daß sie bei der größten zu erwartenden Skalierung gute Werte liefert. Die darunterliegenden Mipmaps werden nicht durch Filterung gewonnen, sondern enthalten entsprechend kleinere Ausschnitte der ursprünglichen Textur mit maximalem Kontrast, so daß die Auflösung praktisch konstant bleibt. Lineare Filterung zwischen den Mipmaps ist zur Vermeidung von sichtbaren Mipmapstufen bei Animation nötig.


Vergleich von Mipmaps durch bilineare Filterung mit Mipmaps aus kontrastkorrigerten Ausschnitten
Alternativ können die Texturkoordinaten dynamisch über deren Gradienten angepaßt werden. Anders als bei Mipmaps wird hier allerdings nicht bei Verdoppelung der Texturkoordinatenänderung auf die nächste Stufe umgestiegen, sondern ein einfacher zu implementierender linearer Zusammenhang zwischen Gradient und gewähltem Texturkoordinatenmultiplikator verwendet:
//skaliere Modulationstextur anhand des sichtbaren Bereichs
//(für annähernd verzerrungsfreies Texturmapping genügt die Analyse einer Komponente):
float TexModFaktor = (1 / ModTexBreite) / length(ddx(TexturMod));
//berechne Koordinaten für grob aufgelöste Stufe:
float2 TexMod1 = TexturMod * (TexModFaktor - frac(TexModFaktor));
//berechne Koordinaten für fein aufgelöste Stufe:
float2 TexMod2 = TexturMod * (TexModFaktor - frac(TexModFaktor) + 1);
//interpoliere zwischen den Stufen:
float Modulation = lerp(tex2D(Modulierer,TexMod1),tex2D(Modulierer,TexMod2),frac(TexModFaktor));
Beleuchtungsberechnung
Da schon im Vertexshader alle zur Beleuchtung nötigen Vertexdaten in Weltkoordinaten transformiert werden sind zur Beleuchtungsberechnung keine weiteren Matrizenmultiplikationen mehr nötig. Nur die noch fehlende Berechnung des Lichtvektors für punktförmige Lichtquellen erfolgt im Pixelshader, so daß die maximale Anzahl der Lichtquellen nur durch die Fähigkeiten der Grafikhardware (maximale Anzahl an Instruktionen und der freier Register für Konstanten) begrenzt wird.
Für die Materialfarbe wird der Fresnelterm mittels der Schlickschen Näherung zu Fresnelfarbe(Einfallswinkel)=Materialfarbe + (1 - Materialfarbe) * (1-Einfallswinkel5) berechnet, die Materialfarbe gilt dabei für senkrecht einfallendes Licht. Auf die Fresnelkorrektur des diffusen Terms wird aufgrund seines bei Metallen geringen Wertes im Vergleich zum spekularen Term verzichtet.
Bei der Implementierung ist wie zuvor beschrieben darauf zu achten, zuerst die skalaren Intensitäten einer Lichtquelle zu berechnen und anschließend mit der Sprühfunktion die lokale Intensität einer Lichtquelle zu bestimmen. Erst dann kann die Summe über die Produkte der resultierenden Intensitäten mit ihren dazugehörigen Material- und der Lichtfarben gebildet und im Pixel abgelegt werden.
Für das restliche aus der Umgebung stammende Licht wird eine EnvironmentMap-Funktion eingesetzt, die mittels des reflektierten Sichtvektors ausgelesen wird. Da es sich hierbei um eine spekulare Reflexion handelt, wird der ermittelte Lichtwert ebenfalls mit der Fresnel-Materialfarbe multipliziert. Für den Streukegel der Reflexion wird eine leicht berechenbare Näherung angewandt: Es wird der Winkel betrachtet, innerhalb dessen ein vorgegebener Anteil der spekularen Reflexion liegt. Dieser bildet sich (bei isotroper Reflexion) auf der durch alle möglichen Reflexionsvektoren gebildeten Halbkugel als Kreis ab. Für hohe Spekularexponenten wird der Winkel klein, so daß der Durchmesser des Kreises mit dem Winkel in erster Näherung identisch ist. Vergleicht man ein Quadrat mit Kantenlänge d und einen Kreises mit Durchmesser d miteinander, so ergibt sich ein Verhältnis von 1 zu Pi/4 zu 1 (rund 0.79) zwischen Quadrat- und Kreisfläche. Dies bedeutet, für einen Kreis mit Durchmesser d auf der Halbkugel, welcher rund 79% der spekularen Reflexion umfaßt, besteht dasselbe Verhältnis zwischen spekularer Reflexion innerhalb und außerhalb des Kreises wie für den Inkreis eines Quadrats mit demselbem Mittelpunkt und Kantenlänge d, welches die gesamte spekulare Reflexion aufnehmen würde. Somit kann dieses Quadrat zur Simulation der spekularen Streuung herangezogen werden.
Den Durchmesser d erhält man im Phong-Modell mit Spekularexponent n aus Pi / 4 = Integral(Integral((n + 1) / (2 * Pi) * cos(a)n * a, a=0..d/2), 0..2*Pi). Entwickelt man cos(a)n als Reihe, so erhält man in quadratischer Näherung cos(a)n = 1 - n / 2 * x2, und somit Pi / 4 = -1/128 * (n + 1) * n * d4 + 1/8 * (n + 1) * d2 mit der Lösung d = 2 * sqrt((2 * n + 2 + sqrt(4*n2 + 8 * n + 4 - 2 * Pi * n2 - 2 * n * Pi)) / ((n + 1) * n)).
Diese kann für n >> 1 gut über d = 3 / sqrt(n) angenähert werden.
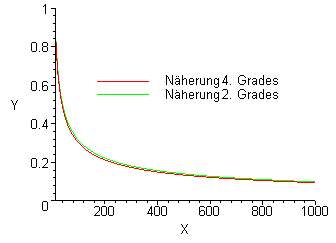
Funktionsverlauf für die exakten Lösungen der Cosinus-Reihenentwicklung quadratischer bzw. vierter Ordnung sowie der beschriebenen Näherung. Die Kurven für die exakte Lösung quadratischer Ordnung und der Näherung sind in der Grafik deckungsgleich.
Die so ermittelte Kantenlänge wird direkt zu Skalierung eines Zufallsvektors in [-1..1]2 orthogonal zum Reflexionsvektor verwendet und diesem hinzuaddiert. Eine weitere Vereinfachung besteht darin, einen im Mittel rund 10% längeren Zufallsvektor unter Verzicht auf Orthogonalität aus [-1..1]3 zu entnehmen - die entstehenden Variationen in der Verteilung fallen praktisch nicht auf.
Ein passender Filter für die Environment Map sollte so gewählt sein, daß ein Texels in etwa eine Fläche in Größenordnung des Kreisradiusses als Durchmesser abdeckt. Bilinear gefilterte Mipmaps bieten sich somit an. Die Wahl der Mipmapstufe kann direkt über den berechneten Kreisdurchmesser erfolgen oder der Graphikhardware überlassen werden. Letzteres ist zwar implementierungsspezifisch, lieferte aber auf den getesteten Karten in Verbindung mit einem Mipmapbias-Wert von etwa -0.5 vergleichbare Ergebnisse.
//Environment Map
float IntensitaetEnvmap = 1; //winkelunabhängig, da schon im Fresnelterm berücksichtigt
float Streuweite = saturate(3 / sqrt(Spekularexponent));
float4 RefFarbeEnv = SpekulareFarbeFresnel * LichtfarbeEnv;
float3 EnvreflektVekt = ReflektVekt + Spruehparameter.xyz * Streuweite;
float4 EnvAnteil = RefFarbeEnv * EnvFarbe(EnvreflektVekt) * IntensitaetEnvmap;
Pixel+= EnvAnteil;
Glanzlichter
Die spekulare Intensität wird mit denselben Funktionen wie das normale Bild berechnet. Ihr Wert kann anschließend entweder zusammen mit dem normalen Bild im Alphakanal oder in einer Multielementtextur gespeichert werden. Oder sie wird mit einem separaten, nur die Intensitätsberechnungen enthaltenden Shader in einem zweiten Durchgang in eine separate Textur gerendert. In diesem Fall kann die Auflösung der erzeugten Textur je nach erwünschter Genauigkeit geringer ausfallen. Falls möglich, sollte zusätzlich noch der Wert aus der Modulationstextur für den nachfolgenden Durchgang mit abgespeichert werden.
Der zweite Durchlauf läuft ausschließlich im Bildraum ab und benötigt dazu neben der spekularen Textur nur noch ein bildfüllendes Rechteck als Eingabe für den Vertexshader. Für den Offset wird die Richtung der ersten Lichtquelle verwendet, da keine genaueren Daten auf Vertexbasis verfügbar sind. Die berechneten Pixel können dann per additivem Alphablending dem Bild hinzugefügt werden.
Der dazugehörige Pixelshader liest pro Pixel 4 Werte im Umkreis Spitzlichtweite eines Pixels aus und gewichtet diese anhand ihres Abstands zum Mittelpunkt. Die Position des Effekts kann dabei um Spitzlichtoffset in Richtung der hellsten Lichtquelle (oder auch einer anderen Vorzugsrichtung) verschoben werden.
Sterneffekte
Um die Belastung der Graphikkarte zu verringern, werden nur diejenigen Pointsprites in voller Größe gezeichnet, an denen auch eine entsprechende spekulare Reflexion vorliegt. Da in 2.0x-Vertexshadern leider nicht auf die spekulare Textur zugegriffen werden kann, wird stattdessen pro Vertex die spekulare Intensität nochmals berechnet. Nachteilig ist, daß hier im allgemeinen weder die modifizierte Normale noch die Anisotropierichtung verfügbar ist. Anstatt sie in einem Vorverarbeitungsschritt den Vertexdaten hinzuzufügen, begnügt sich der hier gezeigte Ansatz allerdings damit, auf entsprechende Korrekturen zu verzichten. Der dadurch in Kauf genommene Verlust an potentiellen Sterneffekten hält sich für mäßige Anisotropie und Bumpmaps niedriger Amplitude in vertretbaren Grenzen. Die Leseposition in der spekularen Textur wird über die COLOR-Register übergeben, da die Texturkoordinaten bei der Expansion der Pointsprites zu Rechtecken überschrieben werden. Die berechneten Pixel können dann per additivem Alphablending dem Bild hinzugefügt werden.


Teekessel mit und ohne spekulare Vorskalierung der Effektsprites. Der einzige Unterschied zeigt sich an dem kleinem Spitzlicht des Henkels. Spekularexponent=533, Isotropie=0.25, Bumpmapvariation unterhalb 5 Grad
Im Pixelshader wird die Sterntextur nur noch anhand der automatisch generierten Texturkoordinaten ausgelesen und mit dem Wert aus der spekularen Textur multipliziert. Damit ist zugleich die Verdeckung nicht sichtbarer Reflexe erledigt.
Definitionen und Begriffe
- Anisotropie
- Eigenschaft, die in Bezug auf Metalloberflächen die Abhängigkeit des Reflexionsverhaltens von der Orientierung des einfallenden Lichtes parallel zur Oberfläche kennzeichnet. Der hier betrachte Fall einfacher Anisotropie kann durch Angabe einer Hauptrichtung sowie die Stärke der Anisotropie vollständig spezifiziert werden.
- Blinn-Phong-Modell
- Empirisches Modell, welches eine Modifikation des Phong-Modells darstellt und den Intensitätsverlauf des gerichtet-diffusen Anteils stattdessen als Funktion des Winkel zwischen der Oberflächennormale und dem Halfwayvektor zwischen Lichtstrahl und Sichtrichtung modelliert.
- Billboard
- Zweidimensionale Figur, dessen Position der eines in Bildkoordinaten transformierten Vertexes entspricht. Je nach Verwendungszweck wird die Größe der Figur anhand der Z-Position in Kamera- oder Projektionskoordinaten skaliert. Die Texturkoordinaten der Figur sind dabei unabhängig von der Position in Bildkoordinaten der Position in der Figur fest zugeordnet.
- BRDF
- Eine BRDF (Bi-directional Reflectance Distribution Function) beschreibt das Verhältnis von reflektiertem zum pro Raumwinkelelement einfallenden Licht an einem Punkt auf einer Oberfläche. Als Parameter werden die Richtungen des einfallenden und des reflektierten Lichtes verwendet, so daß sich im Allgemeinen eine vierdimensionale Funktion und für isotrope Oberflächen eine dreidimensionale Funktion der Einfallswinkel und Reflexionsrichtung ergibt:
BRDF(EinfallswinkelPolar,EinfallswinkelAzimuthal,ReflexionswinkelPolar,ReflexionswinkelAzimuthal) = ReflektierteIntensität / (EinfallendeIntensität * cos(EinfallswinkelPolar) * Raumwinkelelement)
Die Abhängigkeit des Reflexionsverhaltens von der Farbe des einfallenden Lichts wird üblicherweise dadurch berücksichtigt, indem man mehrere skalare BRDFWellenlänge(EinfallswinkelPolar,EinfallswinkelAzimuthal,ReflexionswinkelPolar,ReflexionswinkelAzimuthal)
für jeweils monochromatisches Licht zu einer Vektorfunktion BRDF(EinfallswinkelPolar,EinfallswinkelAzimuthal,ReflexionswinkelPolar,ReflexionswinkelAzimuthal)
für alle Farben zusammenfaßt.
- Farbe
- Eigenschaft des Lichts, gekennzeichnet durch die Verteilung der enthaltenen Wellenlängen. Als Eigenschaft einer Oberfläche mit der Farbe des von ihr reflektierten weißen Lichts identisch
- Filterkern
- Ein Filterkern gibt an, wie sich der gefilterte Wert eines Punktes aus den Werten der umgebenden Punkte errechnet. Für die gängigste Realisierung als gewichtete Summe über endlich viele benachbarte Punkte ist er durch Angabe der endlich vielen Wichtungsfaktoren vollständig spezifiziert.
- Frac(x)
- Nachkommaanteil von x
- (relative) Intensität
- Relative Intensitäten geben den Anteil an einer dazugehörigen Gesamtintensität an, liegen also stets innerhalb [0..1]. Intensitäten kommen als Maß der Stärke des einfallenden bzw. reflektierten Lichts oder der von Pigment bedeckten Oberfläche vor.
- Geordnetes Dithering
- Quantisierungsverfahren, um beliebige Eingabewerte anhand eines Vergleichswerts auf vorgegebene diskrete Werte abzubilden. Dabei hängt der Vergleichwert nur von der Position des Eingabewerts ab und kann somit als Textur gespeichert werden.
- HDR-Rendering
- Verfahren, welche auch Helligkeitswerte außerhalb des Intervalls [0..1] zulassen. Diese werden anschließend durch eine nichtlineare Abbildung (z.B. Addition von Werten außerhalb des Bereichs nach Tiefpaßfilterung, anschließende Gammakorrektur) wieder in den Bereich [0..1] abgebildet.
- Koordinatensysteme
- Tangentialkoordinaten
- Lokales 2D-Koordinatensystem auf der Oberflächenebene eines Objekts. Zur alleinigen Angabe von Richtungsvektoren genügt die Angabe eines Tangential- sowie eines Binormalenvektors für jeden Vertex, der Nullpunkt kann über Texturkoordinaten angegeben werden. Wird im Shader zur Angabe der Anisotropieachsen, Texturkoordinaten sowie Offsetvektoren verwendet. Erweiterung zu einem 3D-Koordinatensystem wird durch Hinzunahme der Oberflächennormale ermöglicht.
- Objektkoordinaten
- Lokales 3D-Koordinatensystem, in welchem die Ortsvektoren, Tangenten, Binormalen sowie Normalenvektoren der Vertices eines einzelnen Polygonmodells vorliegen. Die Ortsvektoren werden durch eine vierte, konstante Komponenten (in D3D = 1) zu einem 4D-Vektor in homogenen Koordinaten erweitert.
- Weltkoordinaten
- Globales homogenes 4D-Koordinatensystem, in welches die Objekte durch Translation, Rotation, Skalierung und ggf. Projektion in der kompletten darzustellenden Szene positioniert werden. In diesen Koordinaten liegen auch Richtungen und Positionen der Lichtquellen vor.
- Kamerakoordinaten
- Globales homogenes 4D-Koordinatensystem, in dem die X und Y-Achsen parallel zur Bildebene vorliegen. Der Betrachter steht im Ursprung des Koordinatensystems, seine Sichtrichtung entspricht der positiven Z-Achse.
- Projektionskoordinaten
- Globales 4D-Koordinatensystem, in welchem die in Kamerakoordinaten vorliegenden Positionsdaten entsprechend der verwendeten Projektion vorbereitet werden. Für perspektivische Projektion entspricht die W-Koordinate nach Transformation der Z-Koordinate in Kamerakoordinaten, bei orthogonaler Projektion einer Konstante. In Porjektionskoordinaten liegen die X- und Y-Komponenten der Ortsvektoren entsprechend des Sichtbereiches skaliert vor, die Z-Komponente wird so skaliert, daß die sichtbaren Werte innerhalb [0..1] liegen.
- Bildkoordinaten
- Globales 2D-Koordinatensystem, in welchem die X- und Y-Komponenten der Ortsvektoren nach der perspektivischen Division vorliegen. Dieses Koordinatensystem ist mit dem des Bildschirms bzw. des Rendertargets identisch.
- Mikrofacette
- Perfekt spiegelnder ebener Bereich beliebig kleiner Oberfläche, der zur Modellierung nicht perfekt spiegelnder, rauher Oberflächen verwendet wird. Das Reflektionsverhalten der Gesamtoberfläche ergibt sich (bis auf einen farbabhängigen skalaren Faktor) vollständig aus der Verteilung der Facettennormalen.
- Modulo-Zufallsgenerator
- Psuedozufallsgenerator der Form xn+1:=(xn * a + b) mod c mit geeigneten Parametern a, b, c, x0
- Phong-Modell
- Rein empirisch begründetes Modell, welches den Intensitätsverlauf des spekularen Term genannten gerichtet-diffusen Anteils des reflektierten Lichts als Funktion des Winkels zwischen einfallendem Lichtstrahl und der an der Oberfläche gespiegelten Sichtrichtung modelliert: SpekularerTerm ~ Saturate(cos(Spekularwinkel))Spekularexponent
Der ungerichtet-diffuse Anteil, diffuser oder Lambertscher Term genannt, ist eine Funktion des Winkels zwischen einfallendem Licht und der Oberflächennormale: DiffuserTerm ~ Saturate(cos(Einfallswinkel))
Das fertige Phong-Modell besteht aus der Summe dieser beiden Terme.
- Pigment
- Material zur Erzeugung von Oberflächen mit bestimmter Farbe
- Pointsprite
- Als Punkt gerenderter Vertex, der durch Aktivieren von D3DRS_POINTSPRITEENABLE von Direct3D im Bildraum zu einem Quadrat mit automatisch generierten Textukoordinaten erweitert wird. Die Achsen des Quadrats entsprechen denen des Bildkoordinatensystems, die Seitenlänge des Quadrats wird im Vertexshader berechnet. Die generierten Texturkoordinaten bilden eine Textur achsenparallel auf das Quadrat ab und liegen innerhalb [0..1]2.
- Saturate(x)
- Saturate(x) := Median({0,x,1})
- Strahlenoptik
- Teilbereich der Optik, in dem die Ausbreitung des Lichtes durch senkrecht zur Wellenfront der Lichtwellen stehende Linien (Lichtstrahlen) beschrieben wird. Auf diese Weise ist eine einfache geometrische Beschreibung und Berechnung möglich, welche in der Praxis als Näherung ausreichend genaue Ergebnisse liefert. Bedingung dafür ist allerdings, daß die beteiligten Strukturen keine Variationen auf Größenordnung der Lichtwellenlänge aufweisen dürfen.
- Vektoren
- Vektoren werden in den beschriebenen Formeln durch Fettschrift kenntlich gemacht. Für Addition a + b und Skalarprodukt a.b = dot(a,b) zweier Vektoren gelten die üblichen Regeln der linearen Algebra, eine Multiplikation a*b wird wie die Addition komponentenweise durchgeführt. Skalare Werte werden ebenfalls wie Vektoren behandelt, wobei fehlende Komponenten durch Wiederholung der existierenden Komponente ergänzt werden.
2D-Vektoren werden für Textur-/Tangential- und Bildkoordinaten verwendet, 3D-Koordinaten enthalten RGB-Farbwerte, Richtungsvektoren, Normalenvektoren sowie Positionsdaten. 4D-Koordinaten werden für homogene Ortskoordinaten und xRGB-Farbwerte verwendet.
- Zufallsdichte
- Funktion, welche diskreten Zufallswerten die Häufigkeit ihres Auftretens zuordnet. Für unendlich viele, dicht geordnete Zufallswerte geht sie in eine kontinuierliche Funktion über. Diese ist so normiert, daß ihr Integral über alle Zufallswerte 1 ergibt.
- Zufallsfunktion
- Monoton steigende Funktion mit Werten zwischen 0 und 1, deren Verlauf die Verteilung dazugehöriger Zufallswerte festlegt. Ihre Ableitung ist die Zufallsdichte.
Quellenverzeichnis
- [1]
- W.R.Cramer: Airbrush und Autolackdesign. Ravensburger Buchverlag, 1992, ISBN 3-473-48022-3
- [2]
- M.F.Canal(Hrsg.): Airbrush. Edition Michael Fischer, 2003, ISBN 3-933033-77-2
- [3]
- J.M.Parramón, M.Ferrón: Das große Technikbuch Airbrush. Edition Michael Fischer, 1992, ISBN 3-924433-80-1
- [4]
- C.M.Mette: Airbrush: Eine Einführung. Ravensburger Buchverlag, 1988, ISBN 3-473-48016-9
- [5]
- C.M.Mette: Airbrush: Eine Fortsetzung. Ravensburger Buchverlag, 1989, ISBN 3-473-48020-7
- [6]
- J.Martin: Airbrush Technik, Metall-Effekte. Edition Michael Fischer, 1990, ISBN 3-924433-84-4
- [7]
- W.Nolting: Grundkurs Theoretische Physik 3 Elektrodynamik. Friedr. Vieweg & Sohn Verlagsgesellschaft, 1997, ISBN 3-528-16933-8
- [8]
- Wissenschaft-Online: Lexikon der Optik: Metalloptik. http://www.wissenschaft-online.de/abo/lexikon/optik/2003
- [9]
- Wissenschaft-Online: Lexikon der Optik: Reflexion. http://www.wissenschaft-online.de/abo/lexikon/optik/2786
- [10]
- B.Freudenberg, M.Masuch, T.Strothotte: Real-Time Halftoning: A Primitive For Non-Photorealistic Shading. Thirteenth Eurographics Workshop on Rendering, 2002
- [11]
- Steve "Gliebster" Gliebe: Tutorials: Metallic Surface. http://gliebster.com/tutorials/?type=photoshop&tutorial=metal
- [12]
- Daniel Sperl: Künstlerisches Rendering für Echtzeit-Applikationen. Diplomarbeit Fachhochschule Medientechnik und -design Hagenberg, 2003
- [13]
- B.Cabral, L.Leedom: Imaging vector Fields using line integral convolution. Proceedings of SIGGRAPH '93, Computer Graphics, pp. 263-272, 1993
- [14]
- Mathematics:Probability and Statistics:Statistical Distributions:Continuous Distributions:Uniform Sum Distribution. MathWorld, Wolfram Research Inc, http://mathworld.wolfram.com/UniformSumDistribution.html
- [15]
- M.Ashikhmin, P.Shirley: An Anisotropic Phong Light Reflection Model. University of Utah, 2000
- [16]
- A.Gooch, B.Gooch., P.Shirley, E.Cohen: A Non-Photorealistic Lighting Model For Automatic Technical Illustration. Department of Computer Science, University of Utah, 1998
- [17]
- M.J.Kilgard: A Practical and Robust Bump-mapping Technique for Today’s GPUs. NVIDIA Corporation, 2000
- [18]
- A.Schilling: Towards Real-Time Photorealistic Rendering: Challenges and Solutions. WSI/GRIS, Universität Tübingen, 1997
- [19]
- M.Toksvig: Mipmapping Normal Maps. NVIDIA Corporation, 2004
- [20]
- A.S.Shastry: High Dynamic Range Rendering.
- [21]
- DirectX 9.0 Programmer's Reference. Microsoft Corporation, 2002
Anhang

 Beugungssterne und ein skizzierter Horizont sowie Einsatz von Masken, Radierer, Pinsel und Spittering (Quelle:
Beugungssterne und ein skizzierter Horizont sowie Einsatz von Masken, Radierer, Pinsel und Spittering (Quelle:  Hervorragend umgesetzter Chromeffekt, hervorgehoben durch Reflektionen mit hohem Detailgrad und Kontrast (Quelle:
Hervorragend umgesetzter Chromeffekt, hervorgehoben durch Reflektionen mit hohem Detailgrad und Kontrast (Quelle: 
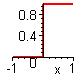 Verwendete Stufenfunktion S(x)
Verwendete Stufenfunktion S(x) Die ursprüngliche Intensität eines Farbverlaufs
Die ursprüngliche Intensität eines Farbverlaufs 1:1 den Pixeln zugeordnete Zufallswerte
1:1 den Pixeln zugeordnete Zufallswerte Pixelweise ausgewertete Differenz x
Pixelweise ausgewertete Differenz x Nach Anwendung von S(x)
Nach Anwendung von S(x)
 Dichte der Stufenfunktion: dS(x)/dx
Dichte der Stufenfunktion: dS(x)/dx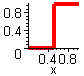 Stufenfunktion S(x)
Stufenfunktion S(x)
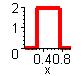 Dichte der Stufenfunktion (w = 1/2): dSlin(x)/dx
Dichte der Stufenfunktion (w = 1/2): dSlin(x)/dx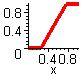 Stufenfunktion Slin(x)
Stufenfunktion Slin(x) Nach Anwendung von Slin(x)
Nach Anwendung von Slin(x)
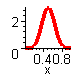 Dichte der Stufenfunktion (w = 1/2): dSlinsum(x)/dx
Dichte der Stufenfunktion (w = 1/2): dSlinsum(x)/dx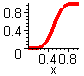 Stufenfunktion Slinsum(x)
Stufenfunktion Slinsum(x) Nach Anwendung von Slinsum(x)
Nach Anwendung von Slinsum(x)
 Darstellung von Slinsum(x-Intensität) für Intensitäten von 0.5, 0.25 und 0.1
Darstellung von Slinsum(x-Intensität) für Intensitäten von 0.5, 0.25 und 0.1 Darstellung von Slinsum(x-Intensität) für dieselben Intensitäten nach passender Skalierung der Breite
Darstellung von Slinsum(x-Intensität) für dieselben Intensitäten nach passender Skalierung der Breite
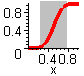 Bei geringerer Varianz überstreicht x einen entsprechend kleineren Teil des Definitionsbereichs von Slinsum(x-Intensität).
Bei geringerer Varianz überstreicht x einen entsprechend kleineren Teil des Definitionsbereichs von Slinsum(x-Intensität).

 Verschiedene Stufenfunktionsbreiten bei hoher Varianz
Verschiedene Stufenfunktionsbreiten bei hoher Varianz
 Verschiedene Stufenfunktionsbreiten bei geringer Varianz
Verschiedene Stufenfunktionsbreiten bei geringer Varianz
 Würfel mit Modulationstextur auf der Oberfläche
Würfel mit Modulationstextur auf der Oberfläche Sprüheffekt mit Modulation auf einem rein ambient beleuchteten Würfel
Sprüheffekt mit Modulation auf einem rein ambient beleuchteten Würfel Derselbe Würfel, leicht gedreht
Derselbe Würfel, leicht gedreht Die Differenz beider Bilder verdeutlicht die Auswirkung auf animierte Bilder
Die Differenz beider Bilder verdeutlicht die Auswirkung auf animierte Bilder
 Modulationstextur nach Zoom auf eine Ecke des obigen Würfels
Modulationstextur nach Zoom auf eine Ecke des obigen Würfels Dieselbe Szene mit dynamisch angepaßten Modulationstexturkoordinaten
Dieselbe Szene mit dynamisch angepaßten Modulationstexturkoordinaten
 Farbcodierte Vektoren (r,g,b) = ((x,y,z,)+1)/2 in Welt- und in Bildkordinaten
Farbcodierte Vektoren (r,g,b) = ((x,y,z,)+1)/2 in Welt- und in Bildkordinaten Errechnete Schraffur
Errechnete Schraffur
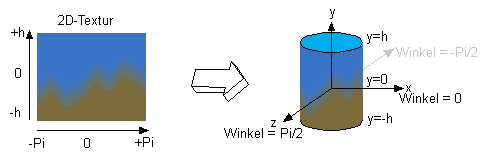








 Würfel ohne und mit nachgezeichneten Kanten
Würfel ohne und mit nachgezeichneten Kanten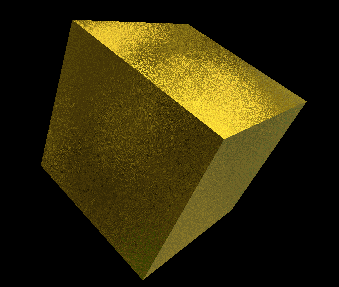
 Würfel mit ebener und unebener Oberfläche via Bumpmap
Würfel mit ebener und unebener Oberfläche via Bumpmap
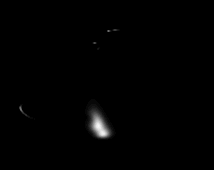









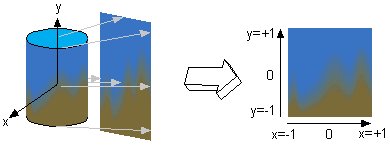


 Funktionsverlauf für die exakten Lösungen der Cosinus-Reihenentwicklung quadratischer bzw. vierter Ordnung sowie der beschriebenen Näherung. Die Kurven für die exakte Lösung quadratischer Ordnung und der Näherung sind in der Grafik deckungsgleich.
Funktionsverlauf für die exakten Lösungen der Cosinus-Reihenentwicklung quadratischer bzw. vierter Ordnung sowie der beschriebenen Näherung. Die Kurven für die exakte Lösung quadratischer Ordnung und der Näherung sind in der Grafik deckungsgleich.



